The graphs \(K_5\) and \(K_{3,3}\) are two of the most important graphs within the subject of planarity in graph theory. Kuratowski’s theorem tells us that, if we can find a subgraph in any graph that is homeomorphic to \(K_5\) or \(K_{3,3}\), then the graph is not planar, meaning it’s not possible for the edges to be redrawn such that they are none overlapping.
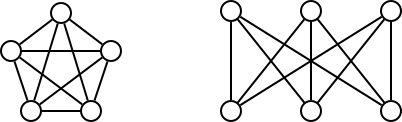
Two nonplanar graphs
Of course, this theorem relies on the fact that \(K_5\) and \(K_{3,3}\) are, themselves, not planar. While it’s pretty easy to see \(K_5\) is not planar, \(K_{3,3}\) is a bit more involved. I’ve read a lot of proofs of this, but frankly I found most of them sorely lacking. Here I try my hand at providing a clearer proof than what you may find elsewhere. Hopefully my explanation will make things click for a Googling student.
Intuition
First I want to simply convince you. This won’t be as formal a proof as I intend to provide, but I want to give a sense of the intuition. I’m a visual learner, so often I find that an informal explanation or a series of examples is more convincing to me personally than a proof.
First, let’s remove three edges from \(K_{3,3}\). This will be a new graph that we’ll call \(G\). The edges we’re removing are going to be the straight vertical edges, the ones that join a vertex with it’s counterpart on the opposite side of the graph (treating the top and bottom as sides). We’ll be adding these back later, but we’re going to remove them for now.
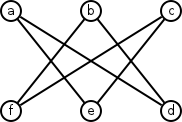
Modified graph G
We’ve also labeled the vertices clockwise from \(a\) to \(f\) for clarity.
Now, it’s easy to see that \(G\) is planar. We can re-arrange the vertices and make a simple hexagon out of the graph.
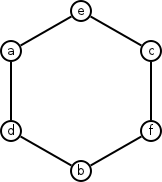
Clearly, \(G\) is planar. But the real question is, what about \(K_{3,3}\) - Remember, we removed three edges from the graph to get \(G\). If \(G\) is planar and \(K_{3,3}\) is not, then it must be impossible to add those three edges back into the graph without having at least two of them overlap.
The edges missing are \((a,f)\), \((b, e)\), and \((c, d)\). You can see that all of of those edges have to cross the middle of the hexagon, so there’s no way to put three, or even two edges into the middle of it without them crossing.
Even going around the outside of the graph doesn’t help. If you put one edge outside and one edge inside, you still have one more edge to reinsert. No matter what, at least two of the three edges are going to have to cross each other. Clearly, \(K_{3,3}\) is not planar.
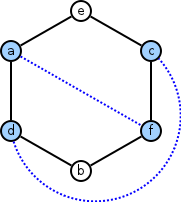
Formal Proof by Contradiction
Intuition is great, but let’s nail down the proof with a bit more mathematical precision. We’re going to do a proof by contradiction.
First, let’s assume for the purpose of contradiction that \(K_{3,3}\) is planar.
If it is planar, then is must obey Euler’s Formula, which is:
\[V - E + F = 2\]for number of vertices \(V\), number of edges \(E\), and number of faces \(F\), which can be rewritten as \(F = E + 2 - V\). In this case, there are 9 edges and 6 vertices, so \(F = 9 + 2 - 6 = 5\), so the number of faces must be five. We’ll come back to this fact in a bit.
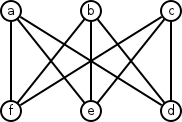
Labeled Graph
So what would it take to have a face in this graph? How many edges would surround any given face? Let’s say we start at some vertex, for example \(a\). We want to walk along edges from vertex to vertex and return to our starting vertex \(a\). If we can do this in a planar graph, we have a face (and remember, we’ve assumed the graph is planar). What’s the smallest number of edges that can get us back to our starting point?
It can’t be one edge, because there are no loops. And it can’t be two edges, because that would mean that there are two edges between two vertices, in other words a multi-edge, and we don’t have any of those either. It also can’t be three edges, because after two edges we’re going to be back on the same side of the graph as our starting vertex, and we know those two don’t connect because the graph is bipartite. For example, if you start at \(a\), moving one edge away puts you at either \(f\), \(e\), or \(d\). Moving another edge away puts you at \(b\) or \(c\) and there’s no way to get back to \(a\) with one more edge. So no face can be surrounded by three edges.
The minimum number of edges needed to draw a face is four. Four edges can get you back to the starting node, creating a face. For example, \(a\) to \(e\) to \(b\) to \(f\) and back to \(a\).
If there are at least four edges per face, then the total number of “face boundaries”, meaning the number of times an edge (any edge) is counted as the border of a face, is at least \(4F\).
Any edge can only sit between two faces (since a face must use an entire edge and cannot use part of one). Thus, each edge can only count twice as a face boundary, so there are at least \(\frac{4F}{2} = 2F\) edges.
We know that \(F = 5\) from earlier, which means the graph must have at least \(2*5 = 10\) edges. \(E \ge 10\), but we know that \(E = 9\). Thus we are left with \(9 \ge 10\), which is obviously not true, so we’ve found a contradiction, Q.E.D.